本文最后更新于 2024年7月19日 晚上
遗传算法的起源与基础
1975年,John Holland 发表了 Genetic Algorithms-Computer programs that “evolve” in ways that resemble natural selection can solve complex problems even their creators do not fully understand by John H. Holland 一文,正式提出了遗传算法(Genetic Algorithm)的概念。
遗传算法是一种元启发搜索方法,其受到自然选择理论启发,通过模拟含有不同编码种群发生交叉(crossover)、突变(mutation)的过程来提高解的多样度(diversity),并构造特定的适应度函数(fitness)和选择(selection)来使解逐渐收敛到最优。对比传统的优化算法,遗传算法在很多难以给出数学表示以及非多项式时间复杂度的问题中有很好的表现,且更不容易陷入局部最优状态。
基本概念
二进制编码
在自然界中,通过基因型表征繁殖,繁殖和突变,基因型是组成染色体的一组基因的集合。在遗传算法中,其为一个连续编码组成的序列,如一个二进制串可以用以构建一个染色体,每一个二进制位代表一个基因位点。

而编码指将一个问题的解(solution)转化为一有序染色体序列表示的过程,以二进制编码为例,对于离散解问题(如0-1Kicknap Problem)可以直接将参数编码为 nd bits长度的染色体,对于连续问题,需要将连续的参数变量映射为 nd 维的0-1向量,即
ϕ:ℜ→(0,1)nds.t. x∈[xmin,xmax]
对于一个 nx 维的解向量 x=(x1,⋯,xj,⋯,xnx), xj∈ℜ,编码后的二进制个体 b=(b1,⋯,bj,⋯,bnx), bj=(b(j−1)nd+1,⋯,bjnd),(bl∈{0,1}),对于编码后的 bj 可以通过映射 Φj:{0,1}nd→[xmin,j,xmax,j] 转换为浮点数
Φj(b)=xmin,j+2nd−1xmax,j−xmin,j(l=1∑nd−1bj(nd−1)⋅2l)
因此可得到编码函数 ϕ(x)=([xmax−xmin(x−xmin)(2nd−1)])dec→bin, 其中取整函数[x]={n∈Z∣argmin∣n−x∣},(x)dec→bin 为进制转换函数。
通过上述计算,会发现二进制编码解码后不能得到精确值,每个参数变量 xj 的精度为 2nd−1xmax,j−xmin,j。
除此以外,二进制编码还会有海明悬崖问题(Hamming Cliff),即当两个十进制数非常近时,他们的二进制数相差很远(eg. (7)10=(0111)2, (8)10=(1000)2),在这里我们定义海明距离(Hamming Distance)如下:
海明距离为两个等长字符串对应位置不同字符的个数。
可以看出,相邻的十进制 7、8 在二进制编码后的海明距离为4。在二进制编码中,如果海明距离变化不均匀,生成的解编码精度下降,搜索过程易导致欺骗性结果或不能有效定位于全局最小值。因此需要改进编码方式以减小相邻值的海明距离。
格雷编码
格雷编码的特点是连续的两个整数所对应的编码之间只有一个码是不同的,其余码位完全相同。他是针对二进制编码海明悬崖问题的改进。对于一个二进制串 b=(b1,b2,⋯,bi,bi+1,⋯,bn), 第 i 位格雷码计算如下
gi={b1bi−1⊕bi,i=1,1<i≤n
其中⊕为异或操作,在布尔代数中表示只有两个输入不同时才输出真(1),否则输出假(0).
例如,将十进制7对应的二进制串0111转换为格雷编码即为0100,将十进制8对应的二进制串1000转换为格雷编码即为1100,海明距离为1,相比于二进制编码大大减小。从他们之间在0-7上的海明距离变化的比较也可看出
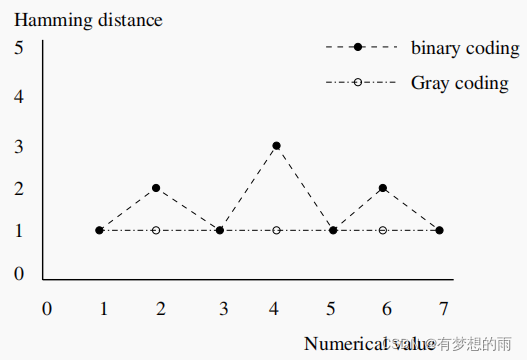
对于格雷编码,解码映射Φj相应的变为
Φj(b)=xmin,j+2nd−1xmax,j−xmin,j(l=1∑nd−1(q=1∑nd−1b(j−1)⋅nd+q)mod2)⋅2l
对于不同类型的问题,染色体的构造与编码方式也不同,应视具体问题而定。
种群(Population)
类似于遗传生物学中的定义,遗传算法中的种群是指含有不同染色体的个体组成的当前代候选解的集合,遗传操作均以种群为单位产生子代,并进行后续的选择操作。
适应度函数(fitness)
适应度函数 f 用于衡量每个个体在当前目标下的生存能力,对于单目标优化问题,它从染色体空间映射到一个实数标量 f:Γnx→ℜ,其中 Γ 代表 nx 维染色体的数据类型。
对于有约束的优化问题,需要在适应度函数 f 中加上惩罚项函数 pC:Γnx→ℜ,以降低越过约束范围个体的生存能力。
选择(Selection)
选择是GA 的主要操作之一,用于产生下一代更好的解个体,主要包含两个步骤:1.选择优良个体用于产生下一代(可直接复制,也可通过父代进行繁殖);2.复制:优良的个体应当有更多的机会被直接复制到下一代,以确保下一代中包含已得到的最优解其中,交叉和复制更加倾向于优良个体,变异倾向于较差的个体。
选择算子
随机选择
每个个体都有 ns 概率进入下一代。
轮盘赌(Roulette Wheel Selection)
对于每个个体,其被选择的概率 φs(xi(t))=∑l=1nsfγ(xl(t))fγ(xi(t)),其中 ns 为种群的个体总数,fγ(xi(t)) 表示 xi 缩放后的适应度函数。
-
对于Minimize问题,其缩放函数为 fγ(xi(t))=γ(xi)=fmax(t)−fΨ(xi(t)),fΨ(xi(t))=Ψ(xi(t)) 为个体 xi 的原始适应度函数,fmax(t) 为第 t 代种群中最大适应度值;或者缩放函数可计算为 fγ(xi(t))=γ(xi)=1+fΨ(xi(t))−fmin(t)1,fmin(t) 为第 t 代种群中最小适应度值。
-
对于Maximize问题,其缩放函数相应为 fγ(xi(t))=γ(xi)=1+fmax(t)−fΨ(xi(t))1。
精英主义(Elistism)
为保证最优解不在遗传操作和选择过程中丢失,我们可以采用将种群中按适应度排序的前 ne 个个体不经过交叉、突变直接复制到子代,这种选择策略称为精英主义或精英保留法。精英群体的个体数 ne 选择得当可以减少种群繁殖代数、提高收敛速度。
锦标赛选择(Tournament Selection)
从个体数为 ns 的种群中随机选择一组个体数为 nts 的群体作为竞赛规模(nts<ns),竞赛规模中适应度最大的个体进入下一代。重复上述操作直至产生的群体个体数与原群体规模相等。
交叉(Crossover)
交叉主要有三种类别:1.无性生殖(一个父代);2.有性生殖(两个父代);3.多重组合(超过两个父代生成一个或多个子代)。
我们考虑有性生殖(即两个父代的情况),染色体编码为二进制编码,交叉方式可分为单点交叉、两点交叉以及均匀交叉。所有的交叉算子基本思想如下所示,x1(t) 和 x2(t) 指被选中作交叉操作的父代,m(t) 为指示父代对应位是否发生交换的掩码。

对于单点交叉,其思想为按概率随机生成一个交叉点,父代染色体在交叉点之后的位置都要发生交换。U(a,b) 指在闭区间 [a,b] 中随机生成一个整数。
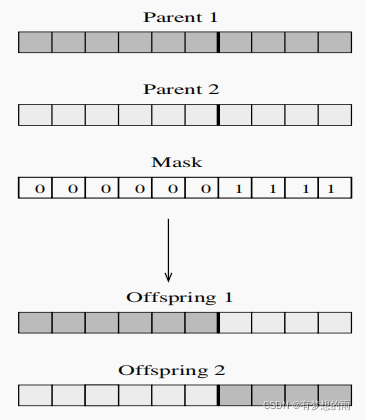

对于两点交叉,其思想为随机生成两个交叉点 ζ1,ζ2(ζ1<ζ2−1), 父代染色体在区间 [ζ1+1,ζ2] 上的位点会发生交换。
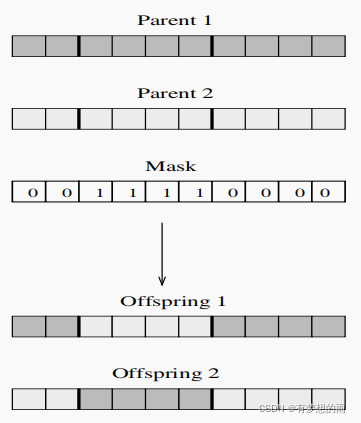

变异(Mutation)
变异的目的是为种群产生新的基因,按突变概率 pm 对子代 x~i(t) 的每个基因进行突变,生成变异个体 xi′(t),pm 一般很小。
在二进制中,若子代 x~i(t) 和变异个体 xi′(t) 的海明距离计为 H(x~i(t),xi′(t)) 则变异个体与原始子代相似的概率为
P(xi′(t))≈x~i(t)=(pm)H(x~i(t),xi′(t))⋅(1−pm)nx−H(x~i(t),xi′(t))
均匀变异
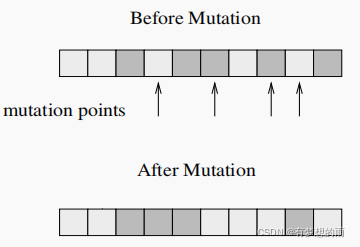

次序变异
次序变异是指按概率生成一个子代的变异位点区间 [ζ1,ζ2] 位于变异区间的位点发生均匀变异。
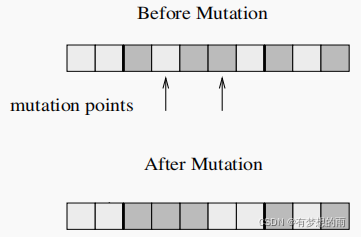

小生境(Niche)
小生境是来自于生态学的一个概念,是指特定环境下的一种生存环境,生物在其进化过程中,一般总是与自己相同的物种生活在一起,共同繁衍后代。
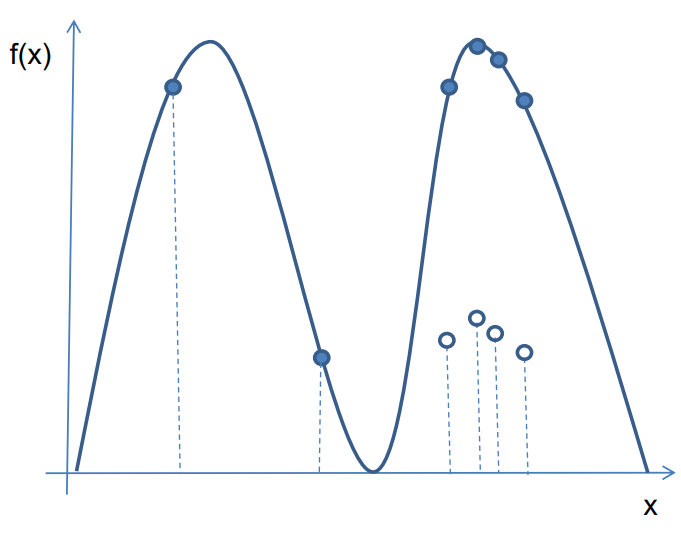
适应值共享(Fitness sharing)
适应值共享算法可以使遗传算法在迭代过程中保持群体多样性,例如在NSGA算法中,经过种群分层每一级非支配层就是一个小生境,每一个非支配解就是小生境中的个体,它们在种群进化过程中逐渐显现出相似的特征(即染色体编码),适应值共享的意义就是降低特征相似的解的适应度。
以NSGA算法中的共享小生境技术为例,假设第 p 级非支配层有 np 个个体,每个个体的虚拟适应度为 fp。
1.首先计算同属一个非支配层的个体 xi 和 xj 的欧几里得距离
dij=l=1∑l=m(Flu−FldFl(xi)−Fl(xj))2
其中 m 为目标个数,Flu,Fld 分别为 Fl 的上界和下界。
2.共享函数(Sharing Function)是用于评估两个个体的相关程度的函数,两个个体 xi 和 xj 间的共享函数 sh(dij)
sh(dij)={1−(σsharedij)α0,dij≤σsharedij>σshare
σshare 是设定的相似度参数,当 xi 和 xj 间欧几里得距离超过该值可认为无共享关系,α 是对相似度函数的修正因子。
3.由此可计算某个个体 xi 与其他同处于一个小生境的个体的累计相似度,称为共享度 ci
ci=j=1∑npsh(dij),i=1,2,...,np
4.计算个体 xi 的共享适应值 fp′(xi)
fp′(xi)=fp(xi)/ci
拥挤距离计算(Crowding Distance)
由于在适应值共享中需要设定 σshare 的值,且需要计算所有个体之间的欧几里得距离并进行比较,复杂度为 O(N2),在NSGA-II算法中对这一小生境技术进行了改进,称为拥挤度算法。在该算法中,需要实现拥挤度和拥挤度比较算子。
拥挤度: 在NSGA-II算法中,每个个体都需要初始化一个拥挤度参数 idistance,对于处于某个非支配层 I 的解 I[i] 来说,拥挤度的计算方法如下
I[i]distance=⎩⎨⎧∞fmax−fminf(I[i+1])−f(I[i−1]),i=0 or ∣I∣,otherwise
其中 ∣I∣ 为非支配层 I 的解的个数,fmax 为该非支配层所有个体目标函数的最大值,fmin 为该非支配层所有个体目标函数的最小值。
拥挤度比较算子: 由于拥挤距离越小表示该个体周围更拥挤,为了保证解迭代过程中的均匀性,定义拥挤度比较偏序关系 ≺n 如下
i≺nj if (irank<jrank)∨(irank=jrank∧idistance>jdistance)
根据该偏序关系可以对群体进行排序,并根据排序筛选进入下一代的个体。
数学原理
虽然遗传算法是基于自然选择学说构建的概念算法,我们可以通过概率论等数学工具分析为什么在迭代过程中群体可以收敛到最优解,这一理论也就是模式定理(Schema Theorery)。以二进制编码为例,对遗传算法应用模式定理分析
通配符(Non-Defining Allele)
在一个由 {0,1,∗} 构成的字符串中,字符 ∗ 称为通配符,可表示 0,1 中的任一字符,属于不确定字符,在字符串中所处的位置称为不确定位。相应的,0,1 是确定字符,所处的位置称为确定位。
模式(Schema)
一个由字符集 {0,1,∗} 构成的串称为一个模式,它表示将其中每个 ∗ 都用 0 或 1 任意替换所得的所有可能的字符串集合,记作 H。例如,H=1∗∗1=1001,1011,1101,1111
模式的阶(Schema Order)
模式 H 中确定字符的个数称为模式的阶,记作 O(H),若 O(H)=n,对应的模式记作 Hn。
串长(String Length)
对某一模式 H,其中所有字符的数量为 l,则该模式的串长 L(H)=l。
定义距(Defining Length)
对某一模式 H,从第一个确定位到最后一个确定位的距离,即最末的确定位位数与最首的确定位位数之差,称为该模式 H 的定义距,记作 δ(H)。例如 H2=∗1∗∗1,δ(H2)=5−2=3.
模式 H 平均适应度 f(H,t)
设 P(t)={X1,X2,⋅⋅⋅,XN} 为第 t 代种群的集合,Eval(Xi) 表示 Xi 的适应度,则第 t 代种群中模式 H 的平均适应度 f(H,t) 可计算为
f(H,t)=∣H∩P(t)∣1x∈H∩P(t)∑Eval(x)
其中,∣H∩P(t)∣ 表示 H 在种群 P(t) 中出现的总数。
模式定理指出,在遗传算子选择、交叉、变异的作用下,具有低阶、短定义距以及平均适应度高于种群平均适应度的模式在子代中呈指数级增长。
也就是说,在种群中对目标函数表现优秀的个体种类,在遗传过程中会保留下来并朝着全局最优解越来越快地收敛。
模式定理证明过程
设经典遗传算法的交叉概率和突变概率分别为 pc 和 pm,模式 H 的定义距为 δ(H),阶为 O(H),对于第 t 代种群进化到 t+1 代的每个遗传操作分析如下
1.选择算子对模式 H 生存期望的影响
根据轮盘赌的操作过程,个体被选中的概率与适应度成正比,则每进行一次轮盘赌,符合模式 H 的个体被选择次数的期望为
E(∣H∩P(t)select∣)=∣H∩P(t)∣⋅∣P(t)∣⋅F(t)f(H,t)=∣H∩P(t)∣⋅F(t)f(H,t)
其中 ∣H∩P(t)∣ 为 P(t) 中符合模式 H 个体的个数,F(t)=∣P(t)∣1∑x∈P(t)Eval(x) 为种群 P(t) 中个体的平均适应度。
上式说明经选择后群体中模式 H 与 f(H,t)/F(t) 有关,当 f(H,t)>F(t) 时,模式 H 的选择期望增加;f(H,t)<F(t) 时,H 的选择期望减少。若设 f(H,t)−F=c×F(c为常数),则上式可改写为
E(∣H∩P(t)select∣)=∣H∩P(t)∣⋅F(t)f(H,t)=∣H∩P(t)∣×(F+c×F)/F=∣H∩P(t)∣×(1+c)
2.交叉算子对模式 H 生存期望的影响
以单点交叉为例,由于单点交叉是随机选择 1 l−1 位置中的某一位作为交叉点,然后交换交叉点后的两父母的对应字串,故只有当交叉点落在 H 的定义距之内的位置,H 才有可能被破坏,但是即使交叉点落在定义距之内的位置,模式 H 仍有不被破环的可能性。
通过上述分析,H 被破坏的概率不超过 pc⋅l−1δ(H),因此经过交叉后,模式 H 的存活概率为
psurvivalc≥1−pc⋅l−1δ(H)
那么,模式 H 在选择、交叉算子共同作用下的生存数量可计算为
E(∣H∩P(t)crossover⋅select∣)≥∣H∩P(t)∣⋅F(t)f(H,t)×psurvivalc=∣H∩P(t)∣⋅F(t)f(H,t)×[1−pc⋅l−1δ(H)]
由上式可知,模式 H 生存数量的变化与平均适应值 f(H,t) 和 δ(H) 有关。
3.变异算子对模式 H 生存期望的影响
考虑均匀变异模式,对变异后的每一个体,其每一个基因位发生变异的概率为 pm,而模式 H 在变异算子的作用下,若要不受破坏 (即生存下来),其确定字符在变异时必须不发生变化,而模式的阶为 O(H),所以根据二项分布,H 不被破坏的概率为 (1−pm)O(H)。
综上所述,经选择、杂交和变异三个遗传算子作用后,下一代种群 P(t+1) 含有 H 中元素个数的期望值应满足
E(∣H∩P(t+1)∣)≥∣H∩P(t)∣⋅F(t)f(H,t)⋅[1−pc⋅l−1δ(H)]⋅(1−pm)O(H)
在实际处理遗传算法的各算子时,我们可以作以下近似:pm≪1,pc≪1,故根据二项展开有 (1−pm)O(H)≈(1−pm⋅O(H)),且
(1−pc⋅l−1δ(H))⋅(1−pm⋅O(H))≈1−pc⋅l−1δ(H)−pm⋅O(H)
代入以上近似,可以得到
E(∣H∩P(t+1)∣)≥∣H∩P(t)∣⋅F(t)f(H,t)⋅[1−pc⋅l−1δ(H)]⋅(1−pm)O(H)≈∣H∩P(t)∣⋅F(t)f(H,t)⋅[1−pc⋅l−1δ(H)−pm⋅O(H)]
由上式,在种群迭代时 (P(t)→P(t+1)),低阶 (O(H) 小),短定义距 (δ(H) 小),平均适应度高于种群平均适应度 (f(H,t)/F(t) 大) 的模式,会在每一代都会增加。
积木块假设
具备低阶、短定义距以及平均适应度高于种群平均适应度特点的模式称为积木块(Building Block),积木块在遗传算子的作用下,相互结合,能生成高阶、长定义距,更高平均适应度的模式,并可最终生成全局最优解。积木块假设解释了为何遗传算法能够在多代后能够收敛到全局最优解,但并不严谨。
具体应用——解决0-1背包问题
0-1背包问题是一种典型的带约束条件的规划优化问题,假设对于一组物品集合 P(下标从 1→n),给定对应重量数组 {w1,w2,…,wn} 以及价值数组 {c1,c2,…,cn}。背包最大重量 W, 背包内物品总价值 C, 要求子物品集合 P′⊆P 满足
maxC=maxP′∑cis.t.P′∑wi≤W
由于对于每个物品 Pi 只有选择放入背包(1)以及不放入背包(0)两种状态,故称为0-1背包问题。解决该类优化问题可以采取遗传算法策略,接下来结合C++代码解释具体实现。
建模与构造遗传算法
染色体设定
正因物品的放入/不放入状态可以记为1/0,我们可以很方便的直接采取二进制编码策略,将物品集合 P 元素的放入状态编码为有序二进制串作为可行解。初始化染色体采取随机生成0-1串,即解 x={x1x2…xi…xn}(xi=1,0),对应代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void GA::init()
{
for (int i = 0; i < pop_size; i++)
{
vector<int> chromosome;
for (int j = 0; j < chromosome_length; j++)
{
chromosome.push_back(rand() % 2);
}
Individual individual;
individual.setChromosome(chromosome);
pop.push_back(individual);
}
}
|
适应度函数
对0-1背包问题来说,每个解对应的物品总价值 P′∑ci 可以直接作为每个解的适应度函数 f(x)=∑i=1nxici。然而在本问题中存在约束项 P′∑wi≤W,我们可以在评估适应度时,对超过约束的解的适应度直接赋值为0,故适应度函数可写为
f(x)=⎩⎨⎧i=1∑nxici0,i=1∑nxiwi≤W,i=1∑nxiwi>W
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void Individual::evaluate()
{
double t_weight = 0;
double t_value = 0;
for (int i = 0; i < (int)chromosome.size(); i++)
{
if (chromosome[i] == 1)
{
t_value += value[i];
t_weight += weight[i];
}
}
if (t_weight > MAX_WEIGHT)
{
fitness = 0;
}
else
{
fitness = t_value;
}
}
|
选择过程
在遗传算法中,轮盘赌策略是最常用的选择策略之一。为了保证每一代最优解不在交叉和变异过程中被破坏,我们也可以结合精英主义法对精英群体进行保留。
根据轮盘赌的原理,每个个体被选择的概率与其适应度成正比,故代码实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| vector<Individual> GA::roulette(vector<Individual> &pop)
{
vector<Individual> new_pop;
vector<bool> isSelected;
for (int i = 0; i < (int)pop.size(); i++)
{
isSelected.push_back(false);
}
double sum = 0;
for (int i = 0; i < (int)pop.size(); i++)
{
sum += pop[i].getFitness();
}
for (int i = 0; i < pop_size - elite_size; i++)
{
double r = (double)rand() / RAND_MAX;
double s = 0;
for (int j = 0; j < (int)pop.size(); j++)
{
s += pop[j].getFitness() / sum;
if (s >= r && !isSelected[j])
{
new_pop.push_back(pop[j]);
isSelected[j] = true;
break;
}
}
}
return new_pop;
}
|
交叉
我们采取两点交叉策略,接受两个父代个体,发生交叉产生两个个体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| vector<Individual> GA::crossover()
{
vector<Individual> offspring;
for (int i = 0; i < (int)pop.size() - 1; i++)
{
for (int j = 1; j < (int)pop.size() ; j++){
if ((double)rand() / RAND_MAX < P_CROSSOVER)
{
vector<Individual> children = Individual::crossover(pop[i], pop[j]);
offspring.push_back(children[0]);
offspring.push_back(children[1]);
}
}
}
return offspring;
}
vector<Individual> Individual::crossover(Individual parent1, Individual parent2)
{
int chromosome_size = parent1.getChromosome().size();
int point1 = rand() % chromosome_size;
int point2 = rand() % chromosome_size;
if (point1 > point2)
{
swap(point1, point2);
}
Individual child1, child2;
vector<int> chromosome1, chromosome2;
for (int k = 0; k < chromosome_size; k++)
{
if (k >= point1 && k <= point2)
{
chromosome1.push_back(parent1.getChromosome()[k]);
chromosome2.push_back(parent2.getChromosome()[k]);
}
else
{
chromosome1.push_back(parent2.getChromosome()[k]);
chromosome2.push_back(parent1.getChromosome()[k]);
}
}
child1.setChromosome(chromosome1);
child2.setChromosome(chromosome2);
return {child1, child2};
}
|
突变
采取均匀突变策略
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| vector<Individual> GA::mutation(vector<Individual> offspring)
{
for (int i = 0; i < (int)offspring.size(); i++)
{
for (int j = 0; j < chromosome_length; j++)
{
if ((double)rand() / RAND_MAX < P_MUTATION)
{
offspring[i].mutate();
}
}
}
return offspring;
}
void Individual::mutate()
{
int pos = rand() % chromosome.size();
chromosome[pos] = 1 - chromosome[pos];
}
|
算法主过程
在每一次种群进化前,采取精英主义保留精英群体,然后使用交叉算子产生子代,经突变、适应度评估后混合进行轮盘赌选择,最后与精英群体合并成为下一代。迭代终止条件为达到设定代数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| void GA::evolve()
{
init();
fitness(pop);
for (int i = 0; i < n_gen; i++)
{
elite = elitism(pop);
vector<Individual> offspring = crossover();
offspring = mutation(offspring);
fitness(offspring);
pop.insert(pop.end(), offspring.begin(), offspring.end());
fitness(pop);
pop = roulette(pop);
pop.insert(pop.end(), elite.begin(), elite.end());
std::cout << "iteration " << i + 1 << " finish." << endl;
}
elite = elitism(pop);
for (int i = 0; i < (int)elite.size(); i++)
{
std::cout << "Elite " << i << " : ";
for (int j = 0; j < chromosome_length; j++)
{
std::cout << elite[i].getChromosome()[j] << " ";
}
std::cout << "Fitness: " << elite[i].getFitness() << endl;
}
}
|
详细代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#ifndef GA_H
#define GA_H
#include <iostream>
#include <vector>
#include <algorithm>
#include <ctime>
#include <cstdlib>
#include <cmath>
#include <fstream>
#include <string>
#define P_MUTATION 0.05
#define P_CROSSOVER 0.85
using namespace std;
class Individual
{
private:
vector<int> chromosome;
double fitness;
public:
Individual();
~Individual();
void setChromosome(vector<int> chromosome);
vector<int> getChromosome();
void setFitness(double fitness);
double getFitness();
void evaluate();
void mutate();
static vector<Individual> crossover(Individual parent1, Individual parent2);
};
class GA
{
private:
int pop_size;
int n_gen;
int elite_size;
int chromosome_length;
vector<Individual> pop;
vector<Individual> elite;
public:
GA(int pop_size, int n_gen, int chromosome_length, int elite_size);
~GA();
void init();
void fitness(vector<Individual> &pop);
vector<Individual> crossover();
vector<Individual> mutation(vector<Individual> offsrping);
vector<Individual> elitism(vector<Individual> &pop);
vector<Individual> roulette(vector<Individual> &pop);
void evolve();
static vector<Individual> sort(vector<Individual> pop);
};
#endif
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
|
#include <iostream>
#include <vector>
#include <algorithm>
#include <ctime>
#include <cstdlib>
#include <cmath>
#include <fstream>
#include <string>
#include "GA.h"
using namespace std;
const double weight[] = { 11 , 24 , 33 , 148 , 9 , 17 , 222 , 57 , 67 , 189 , 47 , 24 };
const double value[] = { 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 };
const double MAX_WEIGHT = 450;
GA::GA(int pop_size, int n_gen, int chromosome_length, int elite_size)
{
this->pop_size = pop_size;
this->n_gen = n_gen;
this->chromosome_length = chromosome_length;
this->elite_size = elite_size;
}
GA::~GA()
{
}
void GA::init()
{
for (int i = 0; i < pop_size; i++)
{
vector<int> chromosome;
for (int j = 0; j < chromosome_length; j++)
{
chromosome.push_back(rand() % 2);
}
Individual individual;
individual.setChromosome(chromosome);
pop.push_back(individual);
}
}
void GA::fitness(vector<Individual> &pop)
{
for (int i = 0; i < (int)pop.size(); i++)
{
pop[i].evaluate();
}
}
vector<Individual> GA::crossover()
{
vector<Individual> offspring;
for (int i = 0; i < (int)pop.size() - 1; i++)
{
for (int j = 1; j < (int)pop.size() ; j++){
if ((double)rand() / RAND_MAX < P_CROSSOVER)
{
vector<Individual> children = Individual::crossover(pop[i], pop[j]);
offspring.push_back(children[0]);
offspring.push_back(children[1]);
}
}
}
return offspring;
}
vector<Individual> GA::mutation(vector<Individual> offspring)
{
for (int i = 0; i < (int)offspring.size(); i++)
{
for (int j = 0; j < chromosome_length; j++)
{
if ((double)rand() / RAND_MAX < P_MUTATION)
{
offspring[i].mutate();
}
}
}
return offspring;
}
vector<Individual> GA::elitism(vector<Individual> &pop)
{
vector<Individual> elite;
vector<Individual> pop_new = sort(pop);
for (int i = 0; i < elite_size; i++)
{
elite.push_back(pop_new[i]);
pop.erase(pop.begin());
}
return elite;
}
vector<Individual> GA::roulette(vector<Individual> &pop)
{
vector<Individual> new_pop;
vector<bool> isSelected;
for (int i = 0; i < (int)pop.size(); i++)
{
isSelected.push_back(false);
}
double sum = 0;
for (int i = 0; i < (int)pop.size(); i++)
{
sum += pop[i].getFitness();
}
for (int i = 0; i < pop_size - elite_size; i++)
{
double r = (double)rand() / RAND_MAX;
double s = 0;
for (int j = 0; j < (int)pop.size(); j++)
{
s += pop[j].getFitness() / sum;
if (s >= r && !isSelected[j])
{
new_pop.push_back(pop[j]);
isSelected[j] = true;
break;
}
}
}
return new_pop;
}
void GA::evolve()
{
init();
fitness(pop);
for (int i = 0; i < n_gen; i++)
{
elite = elitism(pop);
vector<Individual> offspring = crossover();
offspring = mutation(offspring);
fitness(offspring);
pop.insert(pop.end(), offspring.begin(), offspring.end());
fitness(pop);
pop = roulette(pop);
pop.insert(pop.end(), elite.begin(), elite.end());
std::cout << "iteration " << i + 1 << " finish." << endl;
}
elite = elitism(pop);
for (int i = 0; i < (int)elite.size(); i++)
{
std::cout << "Elite " << i << " : ";
for (int j = 0; j < chromosome_length; j++)
{
std::cout << elite[i].getChromosome()[j] << " ";
}
std::cout << "Fitness: " << elite[i].getFitness() << endl;
}
}
vector<Individual> GA::sort(vector<Individual> pop)
{
std::sort(pop.begin(), pop.end(), [](Individual a, Individual b) { return a.getFitness() > b.getFitness(); });
return pop;
}
Individual::Individual()
{
fitness = 0.0;
}
Individual::~Individual()
{
}
void Individual::setChromosome(vector<int> chromosome)
{
this->chromosome = chromosome;
}
vector<int> Individual::getChromosome()
{
return this->chromosome;
}
void Individual::setFitness(double fitness)
{
this->fitness = fitness;
}
double Individual::getFitness()
{
return fitness;
}
void Individual::evaluate()
{
double t_weight = 0;
double t_value = 0;
for (int i = 0; i < (int)chromosome.size(); i++)
{
if (chromosome[i] == 1)
{
t_value += value[i];
t_weight += weight[i];
}
}
if (t_weight > MAX_WEIGHT)
{
fitness = 0;
}
else
{
fitness = t_value;
}
}
void Individual::mutate()
{
int pos = rand() % chromosome.size();
chromosome[pos] = 1 - chromosome[pos];
}
vector<Individual> Individual::crossover(Individual parent1, Individual parent2)
{
int chromosome_size = parent1.getChromosome().size();
int point1 = rand() % chromosome_size;
int point2 = rand() % chromosome_size;
if (point1 > point2)
{
swap(point1, point2);
}
Individual child1, child2;
vector<int> chromosome1, chromosome2;
for (int k = 0; k < chromosome_size; k++)
{
if (k >= point1 && k <= point2)
{
chromosome1.push_back(parent1.getChromosome()[k]);
chromosome2.push_back(parent2.getChromosome()[k]);
}
else
{
chromosome1.push_back(parent2.getChromosome()[k]);
chromosome2.push_back(parent1.getChromosome()[k]);
}
}
child1.setChromosome(chromosome1);
child2.setChromosome(chromosome2);
return {child1, child2};
}
int main()
{
clock_t Begin, End;
double duration;
Begin = clock();
GA ga(14, 15, 12, 4);
ga.evolve();
End = clock();
duration = double(End - Begin) / CLOCKS_PER_SEC;
cout << "tick=" << double(End - Begin) << endl;
cout << "Run Time: " << duration << "s" << endl;
return 0;
}
|












